Let us make the following somewhat bold assumptions about the notion 'friendship':
- there is some clear-cut definition of what it means to be someone's friend (so that for any two persons A and B, we shall never be in doubt whether A's relation to B is one of friendship or not);
- friendship is something that occurs between exactly two persons (such a relation is called 'binary' in a logician's terminology)
- friendship is necessarily mutual; i.e. if A is a friend of B, then B is also a friend of A (such a relation is called 'symmetrical').
(In real life, of course, it may be difficult to find definitions of friendship that would please everyone. And a one-way friendship is certainly conceivable. In that case, the relation is not symmetrical -- just like for instance 'is taller than' or 'has read several books by'. For the former, the relation is in fact what is known as asymmetrical -- it is never mutual, since "A is taller than B" automatically implies that B is not taller than A. For the latter, there is no connection whatsoever between the relation A -- B and the relation B -- A, and perhaps someone would argue that the friendship in real life is of that type as well.)
Now consider the population of a tiny village, ten persons in all (symbolized by circles), and their respective friendship relations (symbolized by arrows).
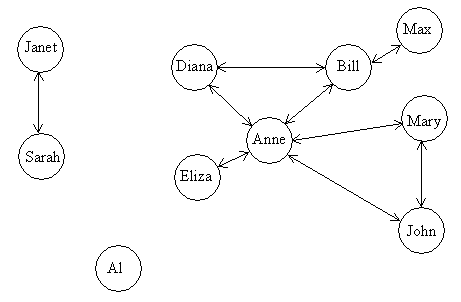
As the figure shows, the objects and their relations (persons and friendship, in this particular case) form a network of nodes and links, respectively. Anne, for instance, is a socially gifted person with five friends whereas Janet and Sarah have no friends but each other. Al, for his part, has no friends at all (and forms a little one-node network of his own).
Such networks based on symmetrical relations occur frequently outside the village of Al and Anne as well (as do other types of networks of less interest to this text). The nodes (objects) might be cities and the links (relations) inter-city connections (e. g. by plane, railway, motorway, or roads in general). Or the nodes might be www servers (with the physical cablework as links), or the chemical reactants and products of the living cell (connected by their respective biochemical reactions).
In the present program, the nodes are not persons nor cities but words in a wordlist, and the relation of interest could possibly be termed "orthographic neighbourship". Such a relationship between two words is at hand if there is a path between them. For "path", then, there are two alternative definitions:
- there is a path from word A to word B if and only if B can be derived from A by adding, replacing or deleting exactly one grapheme
- there is a path from word A to word B if and only if B can be derived from A by replacing exactly one grapheme
The latter definition, of course, corresponds to the "Only consider words of the same length as start and target words..." option. When "replacing" one grapheme with another the replacement is taken from some implicit set, in this case the set of graphemes present in the wordlist. Note that this set does not necessarily coincide exactly with the traditional alphabet -- most wordlists distinguish rosé and lamé from rose and lame, although <é> is not considered a member of the English version of the latin alphabet.
Assuming now (again somewhat boldly) that the English language consists of the following ten words only
dog dig weld wall well dell crop wilt will dwell
, and analysing the English vocabulary as indicated above (with the first definition for "path"), we end up with the following graph. Note that it is structurally identical to the person -- friendship graph above, although the objects and the nature of their relations with one another are very different.
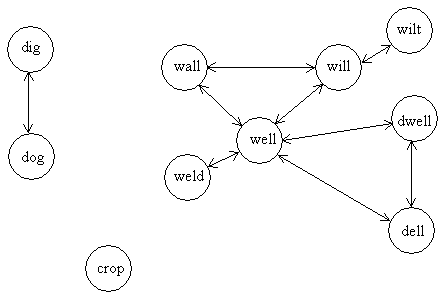
As can be seen, this little language is in fact made up by three separate networks (with our current definitions of the nodes and their relations), containing one, two, and seven nodes respectively. If we supply a start word but no target word, Wordjumper will find all the possible links available. For a start word within the "dig-dog" network, that means exactly two -- from dig to dog and from dog to dig. Any start word pertaining to the "wall" network will similarly yield exactly sixteen steps from A to A (although the exact order of those steps is random).